4.29.4.1 AL/Análisis Básico de Algoritmos. (12 horas) [Nivel Bloom 4]

Referencias Bibliográficas: [Kleinberg and Tardos, 2005,Dasgupta et al., 2006,Cormen et al., 2009,Graham et al., 1994]

Tópicos

1. Análisis asintótico de límites en los casos promedio y superior.
2. Identificar la diferencias entre el comportamiento entre el mejor, mediano y peor caso.
3. Notación Big 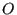$O$, little 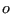$o$, Omega $\Omega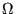$ y Theta $\Theta$.
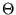4. Clases de complejidad estándar.
5. Medición empírica de desempeño.
6. Puntos de equilibrio entre tiempo vs espacio en algoritmos.
7. Uso relaciones de recurrencia para el análisis de algoritmos recursivos.

Objetivos

1. Explicar el uso de las notaciones Big O, Omega 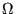$\Omega$ y 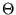Theta $\Theta$ para describir la cantidad de trabajo hecha por un algoritmo.
2. Uso de notaciones Big 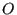$O$, Omega 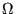$\Omega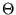$ y Theta $\Theta$ para determinar los límites asintóticos superior, inferior y el más próximo en tiempo y espacio en complejidad de algoritmos .
3. Determinar la complejidad de tiempo y espacio de algoritmos simples.
4. Deducir la relación de recurrencia que describe la complejidad de tiempo de algoritmos definidos recursivamente.
5. Solucionar relaciones de recurrencia elemental.